With how many extra blocks can Carlo make his two solid cubes into a single big one? Further down on this page, you'll get a chance to submit your answer. The picture on the right shows Pierre de Fermat, whose famous "last theorem" says, that -- by themselves -- two whole number cubes can never be combined to make another one. Unfortunately, said Fermat, the book margin he was scribbling on did not allow him to write down the proof of this marvellous fact.

The book in question was the Arithmetica of Diophantos, one of the last great mathematicians of Ancient Greece -- and Fermat himself was one of the first great modern ones. He was active in many areas (for instance, the invention of probability theory), but his greatest contributions were in arithmetic (now usually called number theory) -- which deals with "Diophantine" problems, i.e., those requiring solutions in whole numbers. This apparently harmless sport is a kind of decathlon for mathematicians, drawing from and reflecting to many different fields, and always attracting some of the brightest minds -- many of whom later go on to more concrete things (like Gauss who went from his Disquisitiones Arithmeticae to astronomy and magnetism).

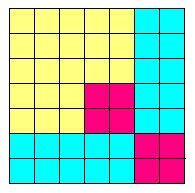
The part of Diophantos's treatise which Fermat was reading in 1637 dealt with the problem of combining two whole number squares into a third one. Here is the recipe: subdivide a square grid as shown, count the yellow tiles (that's your first number) and the green ones (that's your second number); the squares of your two numbers will add up to another square (in this case, 21x21 + 20x20=29x29). Fermat was convinced, that no such thing was possible for cubes, fourth, fifth and higher powers, but he probably had no valid proof, except perhaps in the case of fourth powers.

But Fermat's reputation was such, that each succeeding generation strained its brains to find the missing proof. After the first hundred years, the case of the cubes was settled by Leonhard Euler, the greatest mathematician of his time. A century later, after many partial results (for instance those of Sophie Germain), another great step was taken by Ernst Kummer. So many hunters were involved in this wild goose chase, that it is impossible to list them all here, and the spin-off from their combined efforts was so great that some of it has by now trickled down into each of our lives.

The goose was finally brought down a few years ago by Andrew Wiles (shown on the right), after an ingenious shift of the problem, into the theory of elliptic curves, initiated by Gerhard Frey. Elliptic curves -- so called because they are involved in the computation of arcs in elliptical (e.g., planetary) orbits -- had been well studied over the last two centuries. Although their theory, too, still has big open questions (cf. Swinnerton-Dyer) it contains an arsenal of power tools which Wiles was able to extend to settle Fermat's assertion. Click here for an exciting account of his adventure.

The Pacific Institute for the Mathematical Sciences (PIMS) is a non-profit organisation supported by five universities of Western Canada and dedicated to the promotion of mathematical research -- but it also has a programme of education and public awareness.

This contest is now over. There are infinitely many solutions: 1, 272, 603,..., any number of the form n³-728 with n=9,10,11,... The winner of the draw was Yakov Shklarov.