Full moon at equinox rising over Vancouver. At what time was the photo taken? Further down on this page, you'll get a chance to submit your answer. It involves some skillful guesswork: any answer that falls within 15 minutes of the actual time will be deemed correct. Recall that equinox refers to those special times when day and night are of equal length ("nox" means "night" in Latin). Note that Pacific Standard Time (PST) is about 12 minutes fast for astronomical observations in Vancouver, as this time zone begins about 3 degrees east of here.

The full moon is always opposite the sun (how else would it be full?) -- in other words, 12 hours out of phase. At equinox it should rise when the sun sets, half-way between noon and midnight. For the simplest kind of estimate, you could just work with these ideas, and figure out how much of its journey across the sky the moon seems to have finished when the photo was taken. As a first step of fine-tuning your guess, keep in mind that Vancouver lies about midway between pole and equator; hence sun and moon do not rise straight up but at an angle (as shown at upper right). It also helps to know that both of them cruise across the sky at about one radius per minute. Using more information may not help to get a better answer. For instance, the official moon rise (visibility of the first rays) happens about 5 minutes before the centre of its disc heaves itself over the horizon. All in all, this particular moon was very punctual -- more so than the sun. Fortunately the full moon is not always exactly opposite the sun -- otherwise the earth's shadow would block it out (there would be a lunar eclipse).

The sunset was late that day -- even if we subtract the 5 extra minutes it takes to disappear from view. For the sake of cuckoo clocks and quartz watches (ignorant of the sky) PST pretends that the sun circles the equator at a constant rate. Since it really moves along a slanted plane (the ecliptic), it is normally a few minutes out of step -- sometimes early, sometimes late -- with the time read on a sundial. The diagram on the right shows the reason for this intriguing phenomenon, which is misleadingly called equation of time.

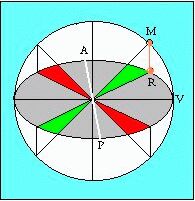
The diagram depicts the plane through the earth's equator. M is the ficticious "mean sun" uniformly circling counter clockwise. The darker ellipse is the projection onto this plane of the actual slanted orbit of the sun, and R is the real sun thus projected. Even if the sun's movement were perfectly uniform and circular, it would look something like this. Obviously the viewing angles differ -- agreeing only four times a year, and otherwise yielding different times on quartz watches and sundials. This basic pattern is complicated by two factors. Firstly, civil clocks start ticking on January 1, while solar ones begin at the vernal equinox V. Secondly, the sun's orbit is not quite circular, but slightly eccentric in the direction of the white line AP. The sun is closest at P (early January) and farthest at A (early July) -- but the difference is only 3.3%.

You can produce the equation of time in your back yard, by planting a pole there and marking its shadow every day at noon quartz time (done more easily in Calgary than in Vancouver). What you'll get is an analemma -- a "figure eight" slimmer in summer than in winter -- showing the difference between mean and solar times. Nothing as simple will allow you to track the moon.

The Pacific Institute for the Mathematical Sciences (PIMS) is a non-profit organisation supported by five universities of Western Canada and dedicated to the promotion of mathematical research -- but it also has a programme of education and public awareness.

This contest is now over. The exact time was 18:35 PST. The winner of the draw was Collin Tsui of Calgary.