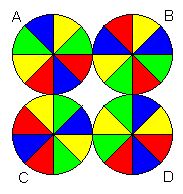
Two slices in each of four styles -- no same ones adjacent. How many ways can you do it? Further down on this page, you'll get a chance to submit your answer. Three different answers will be accepted as correct, because there are three equally legitimate interpretations for the word "ways". They will presently be explained using the diagram on the right.

In that diagram, the "pizzas" A and B differ only by a permutation of the four colours. Since there are 24 such permutations, all our pizzas come in families of 24. The total number of possibilities -- ignoring the important condition that no two adjacent slices have the same topping -- is 105 times 24. Some mystery number, say P, of these 105 families will satisfy that condition. Both P and 24P will be accepted as correct answers. But in some sense, "pizza" C still belongs to the same clan as A, because it can be obtained from it by simple rotation. If you group the P families into such clans, you will get yet another number Q (of clans) which will also count as correct. The "pizza" D in the diagram is not in the same clan as A, B, and C. While every family has 24 members, the size of clans is variable.

Counting things is surely one of the primordial sources of mathematics. Combinatorics has been called the art of "how to count without counting". It is fundamental to statistics and computer science, and has important applications in almost all fields of mathematics (especially number theory, topology, algebra, and discrete mathematics). Many of its problems are easy to state but hard to solve -- and do not require the kind of elaborate theories that make much of mathematics so inaccessible to the novice.

Anyone who still believes that math has formulas for everything will soon learn that combinatorics has no magic bullet. Basic tools which can be helpful include multiplicative counting, the inclusion-exclusion principle, and some group theory (as in Pólya's method). A strongly related field is graph theory, with an extensive literature on colouring -- like the famous Four Colour Problem, which stayed open for about a century until it was finally wrestled down with the help of computers.

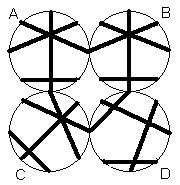The present pizza problem is also about avoiding adjacent colours on a very simple "graph" (an octagon). Since every colour goes on exactly two slices, it can be looked at as studying the ways these slices can be paired up. The diagram on the left shows these pairings without colours. The four patterns represent the same "pizzas" which appear at the top right of this page -- and show more clearly why D does not belong to the same clan as the others.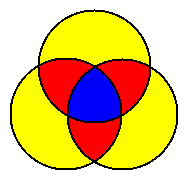

The last of our diagrams is supplied to help the curious reader understand (for p=3) the somewhat formal description of the inclusion-exclusion principle given in the link above. It is not necessary for this problem, but might be useful in certain approaches: if you want to count the total in three overlapping sets, you can first add them all up, but then you must throw out the stuff in the twofold overlaps (it has been counted repeatedly), and finally add the threefold overlap back in again (it has been thrown out repeatedly).

The Pacific Institute for the Mathematical Sciences (PIMS) is a non-profit organisation supported by five universities of Western Canada and dedicated to the promotion of mathematical research -- but it also has a programme of education and public awareness.

This contest is now over. The correct answers were 744 (24P) or 31 (P) or 7 (Q). The winner of the draw was Albert Chan.