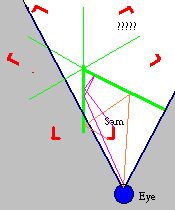
What is the angle between Sam and his middle image, if the one between the mirrors is 59 degrees? Further down on this page, you'll get a chance to submit your answer. The schematic sketch on the right shows the scene from above: the two thick green lines are the mirrors, the white area is the viewer's angle of vision, the thin green lines are imaginay, they serve as orientation aids. The puppet Sam is represented by the red angle near the eye: his reflection in the longer mirror is to the right (back turned to the viewer); his reflection in the shorter mirror is out of sight -- but its reflection in the long mirror is visible as the "middle image" (marked by ?????).

The thin orange and purple zig-zags show the path of the light creating the middle image (knee) and the far left image (hand), respectively. If all such concrete details were left in the picture, it would become impossibly complex. Instead, we consider a kind of abstract reality consisting of Sam and his multiple images, produced by a series of mappings. In three-dimensional space, any plane (e.g, a mirror plane) defines a reflection, which "maps" every point of the space to the point lying on the other side of the plane, at the same distance. Reflections (in assorted planes) can be performed one after the other; two reflections in a row produce a rotation.

Two more mappings are involved in this scenario: the diagram on the upper right shows a projection, the photo on the upper left, a perspective mapping, of three-dimensional space onto two dimensions. Like reflections and rotations, projections are linear, which means that they preserve both straightness and parallelity of lines. Perspective mappings do not respect parallelity (cf., railway tracks pictured below). They are the basis of projective geometry, a subject that was initiated by Renaissance artists. In terms of spatial coordinates, all these mappings are governed by matrices, which may be thought of as higher dimensional multipliers. They have a well-developed algebra, which makes many mind-boggling problems easy enough for computers to handle. They play a crucial role in many applications, e.g., in computer graphics.

Mappings from one structure onto itself are usually called "transformations". The use of mappings and transformations is a salient feature of post-1900 mathematics. A knot, for instance, (cf. diagram on the right) is seen as mapping of a circle into space; knots are important in many fields, from physics to genetics. Modern algebra is dominated by the notion of homomorphism, a mapping from one structure to another which (like the projection above) preserves certain features. Reflections, specifically, are the building blocks for some important symmetry groups -- as was discovered more than half a century ago by H.S.M. Coxeter at the University of Toronto.

The Pacific Institute for the Mathematical Sciences (PIMS) is a non-profit organisation supported by five universities of Western Canada and dedicated to the promotion of mathematical research -- but it also has a programme of education and public awareness.

This contest is now over. The answer was 118 degrees. The winner of the draw was Paige Zanewick.