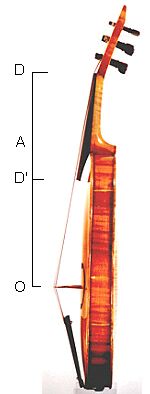
The second string on Mario's violin is tuned to the note D, roughly 300 cycles per second. To make the same string sound a higher note, he shortens it by pressing it against the finger-board. To play "Baa-baa black sheep" he bows "D-D-A-A". The note A is pitched 50% higher than D. What portion of the string (between neck and bridge) must vibrate to produce it? Further down on this page, you'll get a chance to submit your answer.

Pitch is inversely proportional to length of string: the higher the one, the shorter the other. The same goes for the length of tube or pipe in wind instruments, as in the Andean zampoña shown on the right.

If D has 300 cycles per second, A will have 450, and D' will have 600. Our ear hears a doubled pitch, as in D' versus D, as "the same note, but higher" -- and A with 3/2 times the basic pitch is heard "as closely related". These three ratios (1, 3/2, 2) occur in almost all musical scales, but the big gaps on either side of the middle one are filled in differently by different traditions.

The classical major scale uses eight notes related to a basic one (called the "tonic") by the ratios 1, 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, 2. Going from note to note in it, you'll find the increase in pitch to be +1/8, +1/9, +1/15, +1/8, +1/9, +1/8, +1/15. Two of these steps are much smaller than the others and are counted as "semi-tones", but among the "whole tones" there are still two different sizes: +1/8 and +1/9.

This is alright if you can make continuous adjustments as with voice, trombone, violin -- or any of its relatives, like the vielle shown on the left -- but it is disastrous if your instrument has fixed pitches like the zampoña or the organ (its larger cousin) or the guitar with its fixed frets: you could not start your tune on a different note without derailing the scale.  For such instruments, we use a chromatic scale with 12 semi-tone steps, each of which increases the pitch by 5.9463% or roughly 1/17. To approximate the major scale on a guitar, for instance, you take two-two-one-two-two-two-one of these steps (two of them hike the pitch by 12.2462%, a little less than 1/8). This approximation is good enough for most ears, and the new system never gets out of step.

The problem of musical scales is similar to adjusting the rate in compound interest: you are looking for a percentage increase which -- applied repeatedly -- gets close to a given sequence of fractions. In the chromatic scale described above, twelve steps take you to twice, and seven steps close 3/2 times, the basic pitch -- also known as the "tonic".

At a deeper level, this has to do with Diophantine Approximations. To make a scale which reaches the "octave" (twice the tonic) in n equal steps and gets close to the "dominant" (3/2 times the tonic) in k of these, you need to find a fraction k/n which approximates the irrational number log3 / log2 - 1. The standard way of doing this by continued fractions produces the sequence 7/12, 24/41, 31/53 .... The 7/12 corresponds to our chromatic scale, the 31/53 leads to a super-fine scale whose individual steps go up only 1.3164% each time. It is said to have been used in Ancient China. This goes to show: Mathematics is everywhere.

The Pacific Institute for the Mathematical Sciences (PIMS) is a non-profit organisation supported by five universities of Western Canada and dedicated to the promotion of mathematical research -- but it also has a programme of education and public awareness.

This contest is over. The correct answer was 2/3, 0.666..., 67%, and the like. The winner of the draw was Stefan Lukits of Vancouver.