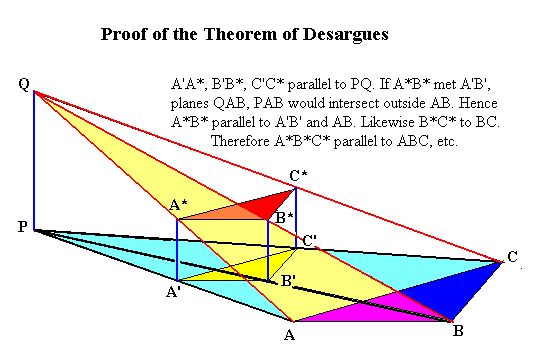

|
The lines AA', BB', CC' lie in a plane and meet in a point P. The segments AB, A'B' and BC, B'C' are pairwise parallel. How does it then follow that AC and A'C' are also parallel? The answer comes from space. Lifting P to some point Q outside the plane (say, vertically), one then constructs a triangle lying above A'B'C' by intersecting planes containing Q and appropriate sides of ABC. The proof is sketched on the diagram, and a more detailed argument is available here as a PDF-file. |